11.3: Normal Probability Plots (2024)

Last updated
Save as PDF

Page ID: 25692

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}}}\)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

To create a normal quantile plot on the TI-83/84

Go into the STAT menu, and then Chose 1:Edit

Figure 11.3.10: STAT Menu on TI-83/84
Type your data values into L1. If L1 has data in it, arrow up to the name L1, click CLEAR and then press ENTER. The column will now be cleared and you can type the data in.
Now click STAT PLOT (\(2^{\text { nd }} Y=\)). You have three stat plots to choose from.

Figure 11.3.11: STAT PLOT Menu on TI-83/84
Use 1:Plot1. Press ENTER.
Put the cursor on the word On and press ENTER. This turns on the plot. Arrow down to Type: and use the right arrow to move over to the last graph (it looks like an increasing linear graph). Set Data List to L1 (it might already say that) and set Data Axis to Y. The Mark is up to you.

Figure 11.3.12: Plot1 Menu on TI-83/84 Setup for Normal Quantile Plot
Now you need to set up the correct window on which to graph. Click on WINDOW. You need to set up the settings for the x variable. Xmin should be -4. Xmax should be 4. Xscl should be 1. Ymin and Ymax are based on your data, the Ymin should be below your lowest data value and Ymax should be above your highest data value. Yscl is just how often you would like to see a tick mark on the y-axis.
Now press GRAPH. You will see the normal quantile plot.

Example 11.3.1 is it normal?

In Kiama, NSW, Australia, there is a blowhole. The data in table #6.4.1 are times in seconds between eruptions ("Kiama blowhole eruptions," 2013). Do the data come from a population that is normally distributed?

Table 11.3.1: Time (in Seconds) Between Kiama Blowhole Eruptions
83	51	87	60	28	95	8	27
15	10	18	16	29	54	91	8
17	55	10	35	47	77	36	17
21	36	18	40	10	7	34	27
28	56	8	25	68	146	89	18
73	69	9	37	10	82	29	8
60	61	61	18	169	25	8	26
11	83	11	42	17	14	9	12

State the random variable
Draw the normal scatterplot.
Do the data come from a population that is normally distributed?

Solution

a. x = time in seconds between eruptions of Kiama Blowhole

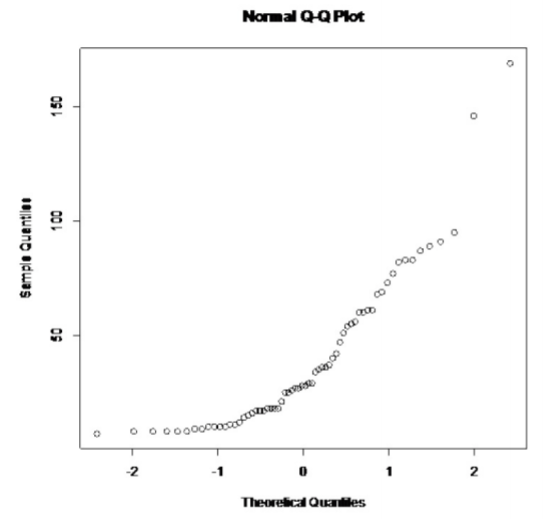
b. The normal scatterplot is in Figure 11.3.15.

Figure 11.3.15: Normal Probability Plot

This graph looks more like an exponential growth than linear.

c. Considering the histogram is skewed right, there are two extreme outliers, and the normal probability plot does not look linear, then the conclusion is that this sample is not from a population that is normally distributed.

Example 11.3.2 is it normal?

One way to measure intelligence is with an IQ score. Example 11.3.2 contains 50 IQ scores. Determine if the sample comes from a population that is normally distributed.

Table 11.3.2: IQ Scores
78	92	96	100	67	105	109	75	127	111
93	114	82	100	125	67	94	74	81	98
102	108	81	96	103	91	90	96	86	92
84	92	90	103	115	93	85	116	87	106
85	88	106	104	102	98	116	107	102	89

State the random variable.
Draw the normal scatterplot.
Do the data come from a population that is normally distributed?

Solution

a. x = IQ score

b. The normal scatterplot is in Figure 11.3.18.

This graph looks fairly linear.

c. Considering the histogram is somewhat symmetric, there are no outliers, and the normal probability plot looks linear, then the conclusion is that this sample is from a population that is normally distributed.

Hypothesis Test on Normality:

A Normal Probability Plot is a scatterplot that show the relationship between a data value (\(x\)-value) and its predicted z-score (\(y\)-value). If the normal probability plot shows a linear relationship and a hypothesis test for \( \rho \) shows that there is a linear relationship, we can assume the population is approximately normal. (Recall from Section 11.3, if two variables do show a linear relationship, then \( \rho \neq 0 \).)

Homework

Exercise 11.3.1

Cholesterol data was collected on patients four days after having a heart attack. The data is in Example 11.3.3. Determine if the data is from a population that is normally distributed.

218 234 214 116 200 276 146

182 238 288 190 236 244 258

240 294 220 200 220 186 352

202 218 248 278 248 270 242

Table 11.3.3: Cholesterol Data Collected Four Days After a Heart Attack
The size of fish is very important to commercial fishing. A study conducted in 2012 collected the lengths of Atlantic cod caught in nets in Karlskrona (Ovegard, Berndt & Lunneryd, 2012). Data based on information from the study is in Example 11.3.4. Determine if the data is from a population that is normally distributed.

48 50 50 55 53 50 49 52

61 48 45 47 53 46 50 48

42 44 50 60 54 48 50 49

53 48 52 56 46 46 47 48

48 49 52 47 51 48 45 47

Table 11.3.4: Atlantic Cod Lengths

Table 11.3.3: Cholesterol Data Collected Four Days After a Heart Attack
218	234	214	116	200	276	146
182	238	288	190	236	244	258
240	294	220	200	220	186	352
202	218	248	278	248	270	242

Table 11.3.4: Atlantic Cod Lengths
48	50	50	55	53	50	49	52
61	48	45	47	53	46	50	48
42	44	50	60	54	48	50	49
53	48	52	56	46	46	47	48
48	49	52	47	51	48	45	47

The WHO MONICA Project collected blood pressure data for people in China (Kuulasmaa, Hense & Tolonen, 1998). Data based on information from the study is in Example 11.3.5. Determine if the data is from a population that is normally distributed.

Table 11.3.5: Blood Pressure Values for People in China
114	141	154	137	131	132	133	156	119
138	86	122	112	114	177	128	137	140
171	129	127	104	97	135	107	136	118
92	182	150	142	97	140	106	76	115
119	125	162	80	138	124	132	143	119

Annual rainfalls for Sydney, Australia are given in Example 11.3.6. ("Annual maximums of," 2013). Can you assume rainfall is normally distributed?

Table 11.3.6: Annual Rainfall in Sydney, Australia
146.8	383	90.9	178.1	267.5	95.5	156.5	180
90.9	139.7	200.2	171.7	187.2	184.9	70.1	58
84.1	55.6	133.1	271.8	135.9	71.9	99.4	110.6
47.5	97.8	122.7	58.4	154.4	173.7	118.8	88
84.6	171.5	254.3	185.9	137.2	138.9	96.2	85
45.2	74.7	264.9	113.8	133.4	68.1	156.4

Answer

1. Normally distributed

3. Normally distributed

FAQs

What is a good normal probability plot? ›

In a normal probability plot (also called a "normal plot"), the sorted data are plotted vs. values selected to make the resulting image look close to a straight line if the data are approximately normally distributed. Deviations from a straight line suggest departures from normality.

Read On ›

What is assessing normality normal probability plots? ›

i) Normal Probability Plots: Look for the observations to fall reasonably close to the green line. Strong deviations from the line indicate non- normality. The observations fall very close to the line. There is very little indication of non-normality.

Discover More Details ›

How to interpret a probability plot? ›

Probability plots may be useful to identify outliers or unusual values. The points located along the probability plot line represent “normal,” common, random variations. The points at the upper or lower extreme of the line, or which are distant from this line, represent suspected values or outliers.

Read On ›

How to interpret a normal plot of residuals? ›

Normal probability plot of residuals

S-curve implies a distribution with long tails.
Inverted S-curve implies a distribution with short tails.
Downward curve implies a right-skewed distribution.
A few points lying away from the line implies a distribution with outliers.

Show Me More ›

How to tell if a normal probability plot is skewed? ›

Right Skew - If the plotted points appear to bend up and to the left of the normal line that indicates a long tail to the right. Left Skew - If the plotted points bend down and to the right of the normal line that indicates a long tail to the left.

What is the normal probability plot used to check? ›

A normal probability plot is a scatterplot of the ranked data values on one axis and the probability that those values come from a normal distribution on the other axis. It can be used to check normality because the points will be close to a horizontal line near 1 if the data are approximately normal.

View Details ›

What is the normal probability plot of the effect estimates? ›

The normal probability plot of the effects shows the standardized effects relative to a distribution fit line for the case when all the effects are 0. The standardized effects are t-statistics that test the null hypothesis that the effect is 0.

Know More ›

How is a normal probability plot used to detect outliers? ›

The line is constructed between observed variable values and normal scores. Outliers and odd values are detected using the probability plot. Normal values are those that fall along the probability line. Outliers are data values that exist outside the pattern (line) of the data.

Get More Info ›

What is a good normality test? ›

The two well-known tests of normality, namely, the Kolmogorov–Smirnov test and the Shapiro–Wilk test are most widely used methods to test the normality of the data. Normality tests can be conducted in the statistical software “SPSS” (analyze → descriptive statistics → explore → plots → normality plots with tests).

What is a normal probability plot quantile? ›

The normal probability plot is one type of quantile-quantile (Q-Q) plot. A Normal Probability Plot compares the values in a data set (on the vertical axis) with their associated quantile values derived from a standardized normal distribution (on the horizontal axis).

Read On ›

What is the p value of the normality plot? ›

If the p value (probability) for the Anderson-Darling statistic is less than 0.05, there is statistical evidence that the data are not normality distributed. If the p value is greater than 0.20, the conclusion is that the data are normally distributed. More data might be needed for values of p between 0.05 and 0.20.

Show Me More ›

What is the purpose of constructing a normal probability plot? ›

A normal probability plot is a graphical technique to assess whether a dataset follows a normal distribution. It plots the quantiles of the dataset against the quantiles of a standard normal distribution. If the data points follow an approximately straight line, it suggests the data is normally distributed.

83	51	87	60	28	95	8	27
15	10	18	16	29	54	91	8
17	55	10	35	47	77	36	17
21	36	18	40	10	7	34	27
28	56	8	25	68	146	89	18
73	69	9	37	10	82	29	8
60	61	61	18	169	25	8	26
11	83	11	42	17	14	9	12

78	92	96	100	67	105	109	75	127	111
93	114	82	100	125	67	94	74	81	98
102	108	81	96	103	91	90	96	86	92
84	92	90	103	115	93	85	116	87	106
85	88	106	104	102	98	116	107	102	89

218	234	214	116	200	276	146
182	238	288	190	236	244	258
240	294	220	200	220	186	352
202	218	248	278	248	270	242

48	50	50	55	53	50	49	52
61	48	45	47	53	46	50	48
42	44	50	60	54	48	50	49
53	48	52	56	46	46	47	48
48	49	52	47	51	48	45	47

114	141	154	137	131	132	133	156	119
138	86	122	112	114	177	128	137	140
171	129	127	104	97	135	107	136	118
92	182	150	142	97	140	106	76	115
119	125	162	80	138	124	132	143	119

83	51	87	60	28	95	8	27
15	10	18	16	29	54	91	8
17	55	10	35	47	77	36	17
21	36	18	40	10	7	34	27
28	56	8	25	68	146	89	18
73	69	9	37	10	82	29	8
60	61	61	18	169	25	8	26
11	83	11	42	17	14	9	12

78	92	96	100	67	105	109	75	127	111
93	114	82	100	125	67	94	74	81	98
102	108	81	96	103	91	90	96	86	92
84	92	90	103	115	93	85	116	87	106
85	88	106	104	102	98	116	107	102	89

218	234	214	116	200	276	146
182	238	288	190	236	244	258
240	294	220	200	220	186	352
202	218	248	278	248	270	242

48	50	50	55	53	50	49	52
61	48	45	47	53	46	50	48
42	44	50	60	54	48	50	49
53	48	52	56	46	46	47	48
48	49	52	47	51	48	45	47

114	141	154	137	131	132	133	156	119
138	86	122	112	114	177	128	137	140
171	129	127	104	97	135	107	136	118
92	182	150	142	97	140	106	76	115
119	125	162	80	138	124	132	143	119

83	51	87	60	28	95	8	27
15	10	18	16	29	54	91	8
17	55	10	35	47	77	36	17
21	36	18	40	10	7	34	27
28	56	8	25	68	146	89	18
73	69	9	37	10	82	29	8
60	61	61	18	169	25	8	26
11	83	11	42	17	14	9	12

78	92	96	100	67	105	109	75	127	111
93	114	82	100	125	67	94	74	81	98
102	108	81	96	103	91	90	96	86	92
84	92	90	103	115	93	85	116	87	106
85	88	106	104	102	98	116	107	102	89

218	234	214	116	200	276	146
182	238	288	190	236	244	258
240	294	220	200	220	186	352
202	218	248	278	248	270	242

48	50	50	55	53	50	49	52
61	48	45	47	53	46	50	48
42	44	50	60	54	48	50	49
53	48	52	56	46	46	47	48
48	49	52	47	51	48	45	47

114	141	154	137	131	132	133	156	119
138	86	122	112	114	177	128	137	140
171	129	127	104	97	135	107	136	118
92	182	150	142	97	140	106	76	115
119	125	162	80	138	124	132	143	119